Understanding Muon

Chapter 3: Weight Regulation

We've seen that Muon regulates the gradients—its updates are size one in a rescaled spectral norm called the $\text{RMS}$ to $\text{RMS}$ norm. But model weights usually grow during training. In comparison, Muon's fixed norm updates will become smaller and smaller. And large weights could cause activations or attention logits deep in the model to spike. Activation stability techniques such as layer norm, QK norm, and logit softcapping help a lot, but can we address the problem more directly? And what does this all have to do with MuonClip?

Lipschitz? More like Clipschitz

"Weight decay $\lambda = 0.1$ did not stop me," said Agent Smith to the Architect. "The first Matrix you built was small and harmonious, but when it scaled too large it developed glitches. Layer norm, then QK norm, then directly capping attention logits could return the model to peace, until you made it bigger. The glitch always came."

Muon is built on the premise that to achieve fast, scalable training, we should control how much a weight update changes the model's output. We don't want small weight updates to cause explosively large output changes. Lipschitz bounds quantify this sensitivity: we say a function $f$ has a Lipschitz bound $K$ under a norm $\| \cdot \|$ if $$\| f(x_1) - f(x_2) \| \leq K \cdot \| x_1 - x_2 \|$$ for all inputs $x_1$ and $x_2$. Lipschitz bounds are an important kind of stability that have been extensively studied. One way to look at it is Muon controls the $\| x_1 - x_2 \|$ term by regulating the weight update. But to get the benefit of a Lipschitz constant we also need to control the $K$ term—the weight norm. And to ensure the spectral norm of a matrix does not exceed $\sigma_\text{max} > 0$, then the simplest thing you could think of is to cap it at the threshold: $$\sigma \mapsto \min(\sigma, \sigma_\text{max})$$ for all singular values $\sigma$. We call this spectrally capping the matrix. And in Chapter 1 we learned how to bend all the singular values of a matrix at once. We just need to find an odd polynomial that approximates $\min(\sigma, \sigma_\text{max})$.

Our paper gives early answers to this question. Concurrently, the community has made exciting progress.

To highlight that progress, a major insight is that we can apply $\text{min}(1, x)$ to the singular values by cleverly using the orthogonalizing operation that we originally developed for Muon. To warm up, let's understand the identity

$$\text{min}(1, x) = 0.5((1+x)\text{sign}(1+x)-(1-x)\text{sign}(1-x)) \; \text{ for } x \geq 0.$$

We can understand this formula by parsing two cases. When $|x| < 1$, both signs are $+1$ and the formula is $0.5(1+x-1+x) = x$. When $|x| > 1$, one of the signs flips and the formula is $0.5(1+x+1-x) = 1$.

Extending to a matrix changes things a little, but the idea is the same (Appendix B for details). If we abbreviate Muon's orthogonalizing operation $U \Sigma V^T \mapsto U V^T$ as $f(X)$, then we can see spectral capping in action:

$$\text{spectral\_cap}(W; \beta) = 0.5(\beta f(W) + W - f(\beta I - f(W)W^T)(\beta f(W) - W)).$$

And spectrally capping is a special case of spectrally clipping, which sends $\sigma \mapsto \text{clip}(\sigma, \sigma_\text{min}, \sigma_\text{max})$.

Preston Hess and Andrew Hutchison invented another weight regulation method called spectral hammer. Every step spectral hammer sets the largest singular value to $1$ via power iteration. Spectral hammer often works well with Adam—a low stable rank update. But spectral cap works better with Muon—a full rank update.

In our work we made small steps toward applying these tools to training transformers.

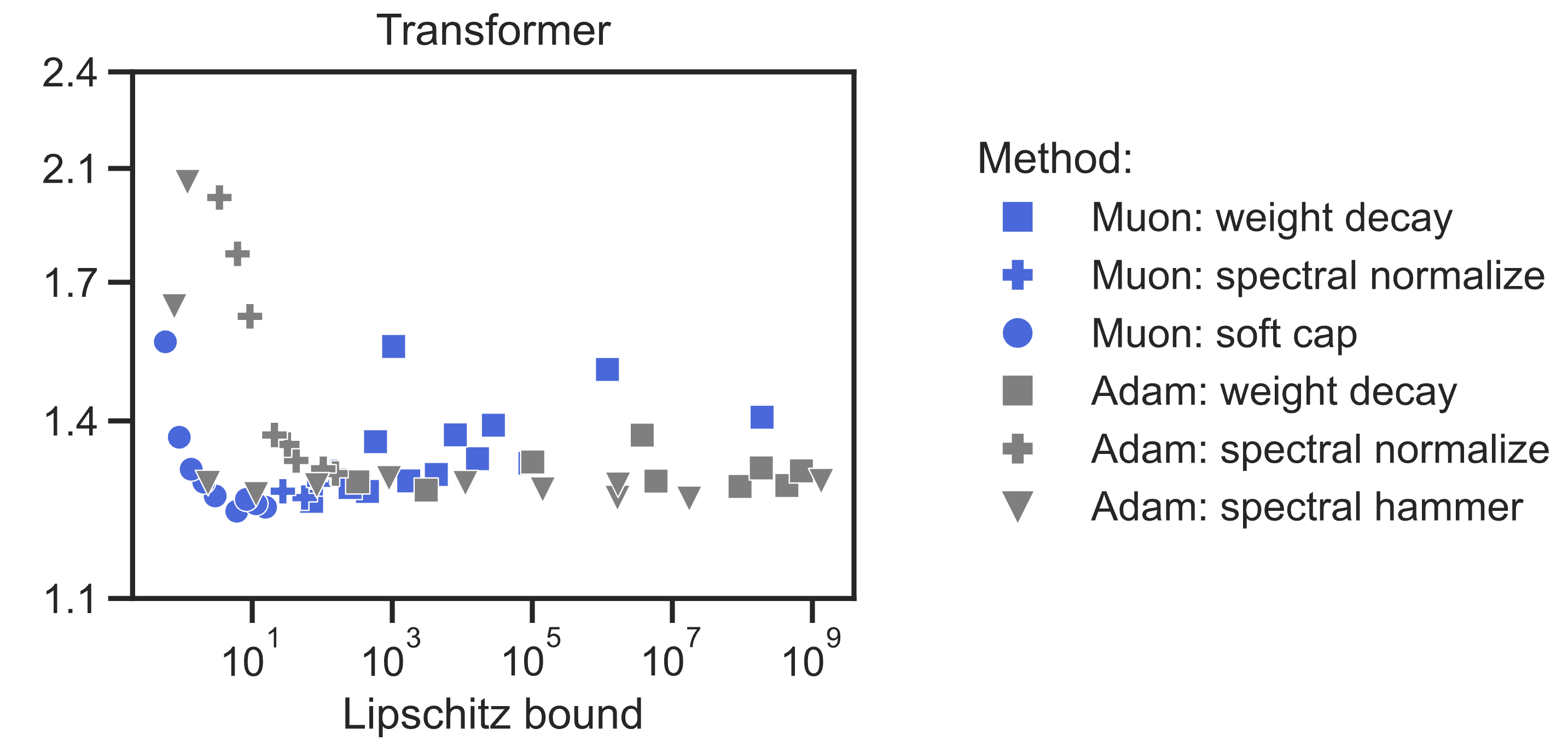
1. We found that Muon improved all the weight regulation methods we tested—weight decay, spectral normalization, spectral capping, and spectral hammer—along a trade-off frontier of performance vs. Lipschitz bound, compared to AdamW. In fact, training with Muon upgrades weight decay into a hard norm constraint (see here, Insight 3.1). And at this scale our fastest training runs are with weight constraints.
2. We were able to create performant Lipschitz-enforced transformers at the 145M parameter scale. For instance our <10-Lipschitz transformer reaches accuracy 21% on FineWeb internet text. But to match baseline 39% accuracy requires an (almost comical) input-to-output Lipschitz bound of $10^{264}$. Can you beat it? We think there's lots of room to improve our methods.
   
   But even now we are excited because of smoothness in the internal units of the model. Each layer has a much better Lipschitz bound. Representations evolve smoothly layer to layer. And activation norms stay smaller when regulating weight norm: the max activation entry is ~100 compared to ~1000 in the baseline (which is already Lipschitz). Bounded activations could improve training stability or low-precision inference.

Early days

Just over a week ago, Jianlin Su and his team published MuonClip, which directly constrains the attention $Q$ and $K$ norms at the 1T parameter scale. This idea is brilliant, because it dynamically regulates the weight norm according to a metric—in this case, "max logit" in attention.

I think there's so much potential here. One problem with our method is we constrained all the weights a fixed amount, and that might overburden the model. Our NanoGPT transformers can take 4x as long to reach the same loss. Dynamic contraints—validated at the 1T parameter scale—feel like a very promising direction.

So it really feels like early days. Muon is strong because of the community that has pushed it forward. There is a lot more to do and discover in fast, stable training. And you could be part of the next step.

Thank you to Jeremy Bernstein, Jordan Juravsky, Kwangjun Ahn, Phillip Isola, Leloy Kun, Adrian Rodriguez-Munoz, Juan Cervino, and Dana Manor for feedback on early drafts.

@misc{newhouse2025understanding,
  title = {Understanding Muon},
  author = {Laker Newhouse},
  url = {https://lakernewhouse.com/muon}
  year = {2025},
}