# Understanding Muon (llms.txt)
Purpose: easy-to-interpret markdown to help an LLM teach the "Understanding Muon" blog series.
Potential use: copy-paste this file (~9.5k tokens) as context into ChatGPT, Claude, Gemini, etc. for asking questions.
Future direction: train a [Cartridge](https://arxiv.org/abs/2506.0626) on that fits in like 4kb but is just as good as this KV cache ;)
## Overview of "Understanding Muon"
This is a three-part blog series written July 2025 whose purpose is to teach the reader about the new deep learning optimizer Muon (MomentUm Orthogonalized by Newton-Schulz).
If the user is asking you to explain something about this material, use best practices in teaching like clear explaining sometimes, asking questions other times.
The blog series gives a bunch of simple ways to understand the principles, math, and intuition behind Muon. Leverage these when you're explaining, but also put your own spin!
Below you'll see each of the chapters formatted in markdown so it's easier for you to read than pure HTML.
## Chapter 1: Into the Matrix (speedy and fun Muon explainer)
"To understand Muon, the first step is to enter the Matrix."
—Not quite Morpheus
We have seen
[a](https://x.com/Kimi_Moonshot/status/1897929976948965870),
[lot](https://arxiv.org/pdf/2505.02222),
[of](https://moonshotai.github.io/Kimi-K2/),
[appreciation](https://x.com/soumithchintala/status/1945297225988354315)
for the Muon optimizer, and excitement that it's been scaled up to training a
[1T parameter model](https://moonshotai.github.io/Kimi-K2/).
A lot of people are learning about Muon for the first time. The first goal of this series is to be a useful guide for those people. But I also think it's a good time to revisit what are the fundamental questions Muon tries to solve, and which ones are still unanswered? I want to argue Muon is only half the picture: not only should we develop good ways to regulate _gradients_, but now there is an opportunity to use similar techniques to regulate the _weights_.
This series proceeds in three parts:
- [Chapter 1: Into the Matrix](https://lakernewhouse.com/writing/muon-1) (speedy Muon explainer based on common confusion points)
- [Chapter 2: Source Code](https://lakernewhouse.com/writing/muon-2) (annotated PyTorch implementation + usage advice)
- [Chapter 3: Weight Regulation](https://lakernewhouse.com/writing/muon-3) (MuonClip, our work, and future directions)
By the end we will see why [Jianlin Su's recent blog on QK-clip](https://kexue.fm/archives/11126) deserves its praise, and why I'm excited about direct, designed weight constraints to guarantee stable training. If you're interested, check out our new paper where we train performant transformers by spectrally regulating the weights, without using activation stability tricks such as layer norm, QK norm, or logit softcapping. This may address a "root cause" of unstable training.
Now let's dive in... to the Matrix. (Or expand more context on Muon.)
Muon is a community effort:
- [Deriving Muon](https://jeremybernste.in/writing/deriving-muon) by Jeremy Bernstein (why Muon is the way it is)
- [Why we chose Muon](https://kexue.fm/archives/10739) by Jianlin Su (more philosophical focus)
- [Muon](https://kellerjordan.github.io/posts/muon/) by Keller Jordan et al. (more speedrun focus)
Our series here is inspired by all three sources above. In addition, this series is about my master's research this year at MIT. Tracing Muon's scholarly history has [many branches](https://docs.modula.systems/intro/reading-list/), including [Shampoo](https://arxiv.org/abs/1802.09568), [spectral descent](https://proceedings.mlr.press/v38/carlson15.pdf), and [duality descent](https://arxiv.org/pdf/1708.00523) all pre-2020. Jeremy Bernstein picked up with his [PhD thesis](https://arxiv.org/abs/2210.10101), [spectral norm work](https://arxiv.org/abs/2310.17813), and [modular norm work](https://arxiv.org/abs/2405.14813), which led to the [optimizer anthology](https://arxiv.org/abs/2409.20325) that we wrote together. The anthology proposed an efficient Newton-Schulz iteration for setting singular values to 1. The iteration inspired Keller Jordan to try the resulting optimizer on two competitive benchmarks, [CIFAR-10 speedrun](https://github.com/KellerJordan/cifar10-airbench) and [NanoGPT speedrun](https://github.com/KellerJordan/modded-nanogpt). Since then, Ashish Vaswani and Jianlin Su showed Muon scales to [large batches](https://arxiv.org/abs/2505.02222) and [up to 1T parameters](https://moonshotai.github.io/Kimi-K2/). Really impressive recent work includes [Dion](https://arxiv.org/abs/2504.05295) (distributed Muon) and [Polar Express](https://arxiv.org/abs/2505.16932) (better polynomials).
My MIT master's thesis (May 2025) is also designed to teach Muon. Its three chapters loosely reflect the three chapters here but are more detailed: intro to Muon, mechanics of Muon, and then weight constraints.
[Check out my thesis](https://lakernewhouse.com/thesis.pdf)
### Neo, The One (in which we see that optimizers like to make updates of size one)
_"You take the blue pill? The story ends, and you believe that a gradient's entries are unrelated numbers."_
_"You take the red pill? You stay in Wonderland, and I show you how deep the rabbit hole goes."_

Let's start with a thought experiment. If the gradient is 10x as large, should an optimizer step 10x as far? Almost the opposite:
- If the loss is $y=(x/100)^2$, the gradients are small, but the model should take big steps.
- If the loss is $y=(100x)^2$, the gradients are big, but the model should take small steps.
As a preview of what is to come, many optimizers therefore take some form of the following advice:
_"No matter how giant or tiny the gradient is, move a fixed distance of one."_
But elementwise optimizers have a limited menu for how to take this advice. The simplest way is SignSGD:
- Instead of SGD: $W_{n+1} = W_n - \eta \cdot G_{n+1}$
- Do SignSGD: $W_{n+1} = W_n - \eta \cdot \text{sign}(G_{n+1})$
where $\eta > 0$ is the learning rate. SignSGD turns every number in the gradient into either $1$ or $-1$.
The Adam optimizer actually reduces to SignSGD when its momentum is turned off. With momentum on, Adam's updates are akin to $\frac{m_1}{\sqrt{m_2}}$, where $m_1$ tracks $G$, and $m_2$ tracks $G^2$ (elementwise square). Its updates resemble $\frac{G}{\sqrt{G^2}} = \text{sign}(G)$, and each _entry_ of its updates hovers near one. Yet Adam looks at entries to step distance one, even though the entries link indirectly to what the weight matrix does in a neural network. [Anthology, Story 1](https://arxiv.org/pdf/2409.20325).
But Muon... it has entered the Matrix. It does not see _entries_ of a gradient matrix. It sees the matrix itself.
And that will be very useful so that Muon can exploit a more sophisticated way to measure "distance one."
A neural network does matrix multiplications (lots of them). Therefore Muon sees the gradients as matrices, unlike Adam which treats every parameter independently. And in the Matrix, there is a lot more you can do.
### The Fundamental Tension (in which a norm defines "size one" for a weight update)
_"When I made the Matrix, I did not force it to choose a measure of size," began the Architect. "I was idealistic then. So for you I chose a norm $\| \cdot \| : \mathbb{R}^{n \times m} \to \mathbb{R}$, and it is how you came to be."_

Why is distance one a good compromise? Because optimizers are constantly struggling against the _fundamental tension_: they want the loss to go down far, but they don't want to disturb the model's output too much; the gradient is only accurate exactly where it is measured. To step a finite distance is always a leap of faith.
But how should we measure how far we are leaping? This is a question Muon innovates on.
Suppose we have single linear layer, $y = Wx$. If we update the weights to be $W + \Delta W$, then how much can the output $y$ change? We'd like a measure of size called $\| \Delta W \|$ where we'd know that $\| y \|$ wouldn't change by more than $\| \Delta W \| \| x \|$. Then even though we actually care about controlling output change, we could get away with controlling the weight update size. So we arrive at a compromise:
$$\underset{\Delta W \text{ s.t. } \| \Delta W \| \leq 1}{\text{argmin}} \langle G, \Delta W \rangle.$$
The compromise says to maximize the alignment between the gradient $G$ and the weight update $\Delta W$, but not step farther than distance one. Otherwise the argmin would flee forever away like $\Delta W = -c \cdot G$ as $c \rightarrow \infty$.
But how do we measure the size $\| \Delta W \|$?
To see, forget that a matrix is made of numbers. Forget that a matrix is called a matrix.
A linear transformation is all there is, $A : \mathbb{R}^{d_\text{in}} \to \mathbb{R}^{d_\text{out}}$. The transformation sends vectors to vectors.
Its inputs are lists of numbers, and we'd like to measure $(\pm 1, \dots, \pm 1)$ as size $1$ no matter how long the list is. That's because we'd like activations in our neural network to have entries around $1$ or $-1$. It's what $\mu\text{P}$ recommends for consistent dimension scaling, and it's the most expressive range for floating point numbers.
But the regular $\ell_2$ norm $\| v \|_2^2 = v_1^2 + \cdots + v_n^2$ will not do, because it judges all-ones vectors differently depending on dimension. Instead we use the root-mean-square norm $\| v \|_\text{RMS}^2 = \tfrac{1}{d} (v_1^2 + \cdots + v_n^2)$.
How much can $A$ change vectors? Imagine the linear transformation takes all vectors $v$ with $\| v \|_\text{RMS} = 1$, and it bends this sphere into an oblong shape. Whichever vector is made the largest, its size will be $A$'s size: $$\| A \|_{\text{RMS} \rightarrow \text{RMS}} := \underset{v : \| v \|_\text{RMS} = 1}{\max} \| A v \|_\text{RMS}.$$
This measure is the $\text{RMS}$ to $\text{RMS}$ norm, the maximum stretch that the $\text{RMS}$ norm can detect. It is a measure of size that accounts for what the matrix actually does in a neural network: transform vectors.
So we arrive back to our compromise, now armed with a specific norm. But what is the solution to
$$\underset{\Delta W \text{ s.t. } \| \Delta W \|_{\text{RMS} \rightarrow \text{RMS}} \leq 1}{\text{argmin}} \langle G, \Delta W \rangle?$$
We can reformulate the constraint using the spectral norm, which measures matrix size via the $\ell_2$ norm: $$\| \Delta W \|_{\text{RMS} \rightarrow \text{RMS}} = \sqrt{\frac{d_\text{in}}{d_\text{out}}} \| \Delta W \|_{\ell_2 \rightarrow \ell_2}.$$
And the spectral norm $\| \cdot \|_{\ell_2 \rightarrow \ell_2}$ will be very useful for us because of its connection to _singular values_.
Every matrix $G \in \mathbb{R}^{d_\text{out} \times d_\text{in}}$ has a singular value decomposition $A = U \Sigma V^T$, where $U$ and $V$ are orthogonal—meaning they preserve a vector's norm—and $\Sigma$ is diagonal with nonnegative entries $\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_n \geq 0$, called the singular values. The spectral norm of $A$ is its largest singular value $\sigma_1$. Here's how we can use that.
Expanding out the SVD, we can write $G = \sum_k \sigma_k u_k v_k^T$, where $u_k$ and $v_k$ are orthonormal vectors. Then
$$\underset{\| \Delta W \|_{\ell_2 \rightarrow \ell_2} \leq 1}{\text{argmin}} \langle G, \Delta W \rangle = \underset{\| \Delta W \|_{\ell_2 \rightarrow \ell_2} \leq 1}{\text{argmin}} \sum_k \sigma_k (u_k^T \Delta W v_k).$$
Now we can argmin each singular vector pair independently because they are orthogonal. For $\Delta W$'s spectral norm not to exceed $1$, each singular value has a budget of $1$. So use it up: set all the singular values to $1$. And keep the singular vectors $u_k$ and $v_k$ the same to maximize alignment. In other words, the solution is $$\Delta W = -UV^T$$ if $G = U \Sigma V^T$. This operation is called _orthogonalizing_. Finally we multiply by $\sqrt{d_\text{out} / d_\text{in}}$ to recover dimension-independence from the $\text{RMS}$ to $\text{RMS}$ norm. (More detail and full proof in [Anthology, Story 2](https://arxiv.org/pdf/2409.20325).)
So we've resolved the fundamental tension. We know the update step—but can we compute it?
### Bend the Singular Values (in which we learn that odd polynomials edit singular values)
_"Do not try to bend the singular values, that's impossible. The direct SVD calculation $$G = U \Sigma V^T \mapsto U f(\Sigma) V^T$$ that sends every singular value $\sigma \mapsto f(\sigma)$ doesn't parallelize well on a GPU. Instead, only try to realize the truth... you don't need to see the singular values to bend them."_

If we could somehow apply a function $f$ to the singular values ("bending the singular values"), then we'd be done: using $f(x) = 1$, we get $U f(\Sigma) V^T = U V^T$. But materializing the SVD isn't friendly to the GPU.
To bend singular values, there's a wonderful trick that Jeremy Bernstein devised in August 2024.
Take the matrix, and cube it! Suddenly, the matrix changes but is still recognizable: $$G^3 := (GG^T)G = (U \Sigma V^T V \Sigma U^T) U \Sigma V^T = U \Sigma^3 V^T.$$
We can take more odd powers, $G^{2k+1} = U \Sigma^{2k+1} V^T$. The odd powers commute straight into the singular values since $V^TV = I$ and $U^TU = I$. Linearity forms up any polynomial $p(x) = a_0x + a_1x^3 + \cdots + a_kx^{2k+1}$ that bends singular values as directly as it bends a single number, without seeing a single one of them: $$\underbrace{p(U \Sigma V^T)}_{\text{acts on matrix}} = \underbrace{U p(\Sigma) V^T}_{\text{acts on numbers}}.$$
With this new power, we do two things. We squash the gradient's singular values into the range $[0, 1]$ by dividing by something certainly bigger than the spectral norm, say $\| G \|_F = \sqrt{\sum_{i,j} G_{ij}^2}$. Then again and again and again we apply some polynomial that will push numbers in the range $[0, 1]$ toward $1$.
Drag the slider to iteratively apply $p(x) = \tfrac{3}{2}x - \tfrac{1}{2}x^3$:





What turns out to matter is how fast the polynomial can push very small $\sigma \ll 1$ toward $1$. Muon uses a $5$ steps of a speedy polynomial with high linear coefficient $3.4445x$, and not converging to $1$ turns out fine in practice.

And let's see what Muon's polynomial does to a real gradient matrix, visualized with singular value histograms:


That's the surprising empirical fact: many gradient singular values are very small. Muon views them equally.
So we've followed the gradient as far as it will go, but only stepping distance $1$. This compromise leads to the map $G \mapsto \sqrt{\tfrac{d_\text{out}}{d_\text{in}}} \; U V^T$ for $G = U \Sigma V^T$, which we compute by iterating odd polynomials since they act directly on the singular values. And the distance we're catering to is fundamentally _matrix-based_. Controlling $\Delta W$ this way controls how much the optimizer update can affect the model output—activation RMS changes by at most $1$.
To recover Muon, we add back the smoothness of momentum, constructing $M_{n+1} = \beta M_n + (1 - \beta) G_{n+1}$ for some parameter $\beta$, typically $0.95$. Muon proposes its core update as orthogonalized momentum:
$$\Delta W_n = \sqrt{\frac{d_\text{out}}{d_\text{in}}} \text{orthogonalize}(M_n).$$
The spoon is bent without having even looked at it. In the next chapter, we'll go through Muon's PyTorch code line-by-line so that you can't get stuck understanding it. And we'll advise on learning rate and when to use Muon.
## Chapter 2: Source Code (annotated PyTorch implementation)
Some of Muon's code can appear puzzling, like the magic numbers $(3.4445, -4.7750, 2.0315)$ in Newton-Schulz. No more being confused: we'll go through the code with line-by-line annotations, including pictures. Afterwards we'll discuss how you can use Muon to get ~1.5x speedups without headaches.
Mouse over the highlights to see explanations.
```python
import torch
# Muon's core idea is to set gradient singular values to one. To do so it will iterate a polynomial five times:
# 
# This is a ~matrix-pilled~ resolution to the _fundamental tension_: the optimizer wants to follow the gradient forever, but it knows that the gradient is only valid exactly where it is measured. So Muon will step distance 1, no matter the size of the gradient.
def set_all_singular_values_to_near_one(G, steps: int):
assert G.ndim >= 2
# These are coefficients of the polynomial $p(x) = 3.4445x - 4.7750x^3 + 2.0315x^5$. This polynomial might look like black magic, but check out this Desmos graph:
# 
# 
# That's what $p(x)$ looks like (left) and what $p(p(p(p(p(x)))))$ looks like (right). Applying $p(x)$ five times is a fast way to send all numbers $x$ to somewhere close to 1, hence (nearly) setting all singular values to 1.
a, b, c = (3.4445, -4.7750, 2.0315)
# We're going to compute a polynomial five times in a row on the gradient matrix $G$. It's numerically stable enough to use a lower precision data type like bfloat16 to speed it up, unlike computing $G^{-1/4}$ which the original Shampoo optimizer update required.
X = G.bfloat16()
if G.size(-2) > G.size(-1):
# This is a computational trick. We'll need to find $XX^T$, which has shape $(n, n)$ if $X$ has shape $(n, m)$. So if $n > m$, we switch them upfront so the inner calculations are smaller. We undo the transpose at the end. And X.mT just means batched transpose, where it will switch the last two dimensions.
# Interested in why it maintains correctness? The polynomial operation might seem complicated, but remember, it's just acting on the singular values. So it is fine to act on the transposed singular values: $p(X^T)^T = (V p(\\Sigma^T) U^T)^T = U p(\\Sigma) V^T$.
X = X.mT
X = X / (X.norm(dim=(-2, -1), keepdim=True) + 1e-7)
for _ in range(steps):
# Step 1. Compute $XX^T$ and save it for later.
A = X @ X.mT
# Step 2. Compute $bX^2 + cX^4$, so that next line we can multiply by $X$ to get $bX^3 + cX^5$.
B = b * A + c * A @ A
# Step 3. Finish up computing $p(X) = aX + bX^3 + cX^5$. Remember what this looks like!   The big idea is we're sending all singular values to 1 in parallel, since odd polynomials commute into the singular value decomposition to act directly on the singular values, $p(G) = p(U \\Sigma V^T) = U p(\\Sigma) V^T$.
X = a * X + B @ X
if G.size(-2) > G.size(-1):
X = X.mT
return X
def muon_update(grad, momentum, beta=0.95, ns_steps=5, nesterov=True):
# lerp does a linear interpolation to set $M_{n+1} = \beta M_n + (1 - \beta) G$, so Muon can smooth out gradients using momentum.
momentum.lerp_(grad, 1 - beta)
# Nesterov momentum is a trick that can help, too. All it does is mix a bigger fraction of the current gradient into the momentum.
update = grad.lerp_(momentum, beta) if nesterov else momentum
# Muon's core operation: set the singular values of the update to 1!
update = set_all_singular_values_to_near_one(update, steps=ns_steps)
# Remember how the spectral norm is prejudiced by dimension? Instead of using it directly, we rescale to use the overall map $G \mapsto \sqrt{\frac{d_\text{out}}{d_\text{in}}} \text{orthogonalize}(G)$ to make the update dimension-independent. This way the input and output spaces are treated with the RMS norm, which views the vectors $(1, 1, 1)$ and $(1, 1, 1, \dots, 1)$ both as having norm 1.
update *= (grad.size(-2) / grad.size(-1))**0.5
return update
# Since Muon is built for matrix parameters, it uses Adam to optimize all other parameters. This function just implements Adam.
def adam_update(grad, buf1, buf2, step, betas, eps):
buf1.lerp_(grad, 1 - betas[0])
buf2.lerp_(grad.square(), 1 - betas[1])
buf1c = buf1 / (1 - betas[0]**step)
buf2c = buf2 / (1 - betas[1]**step)
# Adam's update is $\frac{m_1}{\sqrt{m_2 + \epsilon}}$ where $m_1$ tracks $G$ and $m_2$ tracks $G^2$ (elementwise square). Its updates resemble $\frac{G}{\sqrt{G^2}} = \text{sign}(G)$, and each _entry_ of its updates hovers near one. Yet Adam looks at entries to step distance one, even though the entries link indirectly to what the weight matrix does in a neural network. [Anthology, Story 1](https://arxiv.org/pdf/2409.20325).
return buf1c / (buf2c.sqrt() + eps)
class Muon(torch.optim.Optimizer):
def __init__(self, param_groups):
# The __init__ function sets up some default hyperparameters, including for an internal AdamW optimizer on parameters not designed for Muon. More on that below the source code...
for group in param_groups:
assert "use_muon" in group
# Muon is designed to optimize matrix parameters. All other parameters are optimized with AdamW.
if group["use_muon"]:
# defaults
group["lr"] = group.get("lr", 0.02)
group["momentum"] = group.get("momentum", 0.95)
group["weight_decay"] = group.get("weight_decay", 0)
assert set(group.keys()) == set(["params", "lr", "momentum", "weight_decay", "use_muon"])
else:
# defaults
group["lr"] = group.get("lr", 3e-4)
group["betas"] = group.get("betas", (0.9, 0.95))
group["eps"] = group.get("eps", 1e-10)
group["weight_decay"] = group.get("weight_decay", 0)
assert set(group.keys()) == set(["params", "lr", "betas", "eps", "weight_decay", "use_muon"])
super().__init__(param_groups, dict())
@torch.no_grad()
def step(self, closure=None):
loss = None
# This is a PyTorch feature where you can optionally allow the optimizer to recompute the loss inside the step() function.
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
if group["use_muon"]:
for p in group["params"]:
if p.grad is None:
p.grad = torch.zeros_like(p)
state = self.state[p]
if len(state) == 0:
# Initialize the momentum buffer!
state["momentum_buffer"] = torch.zeros_like(p)
# The update we've all been waiting for!
update = muon_update(p.grad, state["momentum_buffer"], beta=group["momentum"])
p.mul_(1 - group["lr"] * group["weight_decay"])
p.add_(update, alpha=-group["lr"])
else:
for p in group["params"]:
if p.grad is None:
p.grad = torch.zeros_like(p)
state = self.state[p]
if len(state) == 0:
state["exp_avg"] = torch.zeros_like(p)
state["exp_avg_sq"] = torch.zeros_like(p)
state["step"] = 0
state["step"] += 1
update = adam_update(p.grad, state["exp_avg"], state["exp_avg_sq"],
state["step"], group["betas"], group["eps"])
p.mul_(1 - group["lr"] * group["weight_decay"])
p.add_(update, alpha=-group["lr"])
return loss
```
Implementation adapted from [Keller Jordan's GitHub](https://github.com/KellerJordan/Muon).
Now that we have seen Muon's code, let's tackle some FAQs:
1. Which parameters should Muon optimize, and which should be left to AdamW?
Muon is designed for parameters that map dense activations to dense activations—such as the weight matrices in MLPs, attention $(Q, K, V, W)$, convolution kernels, and the final layer of a diffusion model. These are 2D matrices with dense vectors for both input and output. Muon is not designed for elementwise vector parameters such as bias and layer norm scales, or the embedding matrix of a language model. Muon optimizes these other parameters with an AdamW backup.
_Exercise 1: what's wrong with the parameter rule below?_
```python
def is_muon_param(p):
return p.ndim == 2 # incorrect
```
_Solution 1: this rule could misinterpret 2D matrix parameters whose input/output norms aren't RMS, for example an LLM embedding matrix. Since Muon is designed for RMS norms, it may not perform well here._
_Exercise 2: does Muon make sense for the patch embedding matrix of a vision transformer?_
_Solution 2: likely yes, since images are dense vectors with entries $\approx 1$._
2. Should Muon and Adam share the same learning rate?
Not necessarily. If you do share a learning rate, then while the best way to do it may actually be an open question, two approaches are discussed in
[Microsoft's Dion paper](https://arxiv.org/abs/2504.05295)
and
[Moonshot AI's Muon paper](https://arxiv.org/abs/2502.16982).
- Dion's approach: follow the usual dimensional factors that transfer learning rate across width, $\sqrt{d_\text{out}/d_\text{in}}$. Then use the same learning rate across Adam and Muon, except scale down the unembedding layer's learning rate by $1/\sqrt{d_\text{in}}$. More discussion in their Appendix D. For more on "natural norms" that inspired this approach see [Jeremy's spectral condition paper](https://arxiv.org/abs/2310.17813).
- Moonshot's approach: match the RMS norm of Adam's updates with the "RMS norm" of Muon's updates. (Yes, we're stepping out the Matrix for a moment to view the weight update as a vector.) Matching the entrywise update scales may be good default if you want to use Adam-like learning rates (3e-4 anyone?) for both Adam and Muon. If $A$ is an orthogonal matrix, $$\| \text{flatten}(A) \|_{\text{RMS}} = 1/\sqrt{\text{max}(d_\text{out}, d_\text{in})}.$$ An experiment you can try at home is that an Adam update's average RMS norm over 10k steps with Gaussian random gradients is around $0.2$. So Moonshot recommends that Muon's update be $$W_{n+1} = W_n - 0.2 \sqrt{\text{max}(d_\text{out}, d_\text{in})} \cdot \eta \cdot \text{orthogonalize}(M_{n+1}).$$
3. What are good default hyperparameters for Muon?
Muon works well with learning rate around $0.02$, but sweep in logspace to find the best one. Using the $\text{RMS}$ to $\text{RMS}$ norm means Muon's optimal learning rate transfers as model dimension grows, so you can sweep on a smaller model. For momentum, $\beta = 0.95$ works well. Tuning it may not make much difference. Weight decay ($0.1$, $0.01$, or sweep in logspace) becomes important for larger models (>0.5B parameters). For the internal Adam optimizer, $\beta_1 = 0.9$ and $\beta_2 = 0.95$ work well. It may also be promising to replace the internal Adam with an internal Lion optimizer with $\beta_1 = 0.95$ and $\beta_2 = 0.98$.
### What's next?
So far our focus has been on regulating the gradients. But if all we control are the gradients, then during training usually every weight matrix grows. Activations or attention logits deep in the model may spike. Layer norm, QK norm, and logit softcapping are very valuable but are indirect: is it possible to attack the problem at its source?
## Chapter 3: Weight Regulation (our work, and future directions)
We've seen that Muon regulates the gradients—its updates are size one in a rescaled spectral norm called the $\text{RMS}$ to $\text{RMS}$ norm. But model weights usually grow during training. In comparison, Muon's fixed norm updates will become smaller and smaller. And large weights could cause activations or attention logits deep in the model to spike. Activation stability techniques such as layer norm, QK norm, and logit softcapping help a lot, but can we address the problem more directly? And what does this all have to do with [MuonClip](https://moonshotai.github.io/Kimi-K2/)?
[Training Transformers with Enforced Lipschitz Bounds](https://arxiv.org/abs/2507.13338)
### Lipschitz? More like Clipschitz
_"Weight decay $\lambda = 0.1$ did not stop me," said Agent Smith to the Architect. "The first Matrix you built was small and harmonious, but when it scaled too large it developed glitches. Layer norm, then QK norm, then directly capping attention logits could return the model to peace, until you made it bigger. The glitch always came."_

Muon is built on the premise that to achieve fast, scalable training, we should control how much a weight update changes the model's output. We don't want small weight updates to cause explosively large output changes. _Lipschitz bounds_ quantify this sensitivity: we say a function $f$ has a
Lipschitz bound $K$ under a norm $\| \cdot \|$ if $\| f(x_1) - f(x_2) \| \leq K \cdot \| x_1 - x_2 \|$ for all inputs $x_1$ and $x_2$. Lipschitz bounds are an important kind of stability that have been extensively studied. One way to look at it is Muon controls the $\| x_1 - x_2 \|$ term by regulating the weight update. But to get the benefit of a Lipschitz constant we also need to control the $K$ term—the weight norm. And to ensure the spectral norm of a matrix does not exceed $\sigma_\text{max} > 0$, then the simplest thing you could think of is to cap it at the threshold: $\sigma \mapsto \min(\sigma, \sigma_\text{max})$ for all singular values $\sigma$. We call this _spectrally capping_ the matrix.
And in [Chapter 1](https://lakernewhouse.com/writing/muon-2) we learned how to bend all the singular values of a matrix at once. We just need to find an odd polynomial that approximates $\min(\sigma, \sigma_\text{max})$.

Our paper gives early answers to this question. Concurrently, the community has made [exciting](https://leloykun.github.io/ponder/spectral-clipping/#34-spectral-clipped-weight-decay) [progress](https://kexue.fm/archives/11006).
To highlight that progress, a major insight is that we can apply $\text{min}(1, x)$ to the singular values by cleverly using the orthogonalizing operation that we originally developed for Muon. To warm up, let's understand the identity
$$\text{min}(1, x) = 0.5((1+x)\text{sign}(1+x)-(1-x)\text{sign}(1-x)) \; \text{ for } x \geq 0.$$
We can understand this formula by parsing two cases. When $|x| < 1$, both signs are $+1$ and the formula is $0.5(1+x-1+x) = x$. When $|x| > 1$, one of the signs flips and the formula is $0.5(1+x+1-x) = 1$.

Extending to a matrix changes things a little, but the idea is the same (Appendix B for details). If we abbreviate Muon's orthogonalizing operation $U \Sigma V^T \mapsto U V^T$ as $f(X)$, then we can see spectral capping in action:
$$\text{spectral\_cap}(W; \beta) = 0.5(\beta f(W) + W - f(\beta I - f(W)W^T)(\beta f(W) - W)).$$

And spectrally capping is a special case of _spectrally clipping_, which sends $\sigma \mapsto \text{clip}(\sigma, \sigma_\text{min}, \sigma_\text{max})$.
Preston Hess and Andrew Hutchison invented another weight regulation method called _spectral hammer_. Every step spectral hammer sets the largest singular value to $1$ via power iteration. Spectral hammer often works well with Adam—a low stable rank update. But spectral cap works better with Muon—a full rank update.
In our work we made small steps toward applying these tools to training transformers.
- We found that Muon improved all the weight regulation methods we tested—weight decay, spectral normalization, spectral capping, and spectral hammer—along a trade-off frontier of performance vs. Lipschitz bound, compared to AdamW. In fact, training with Muon upgrades weight decay into a hard norm constraint (). And at this scale our _fastest_ training runs are with weight constraints.
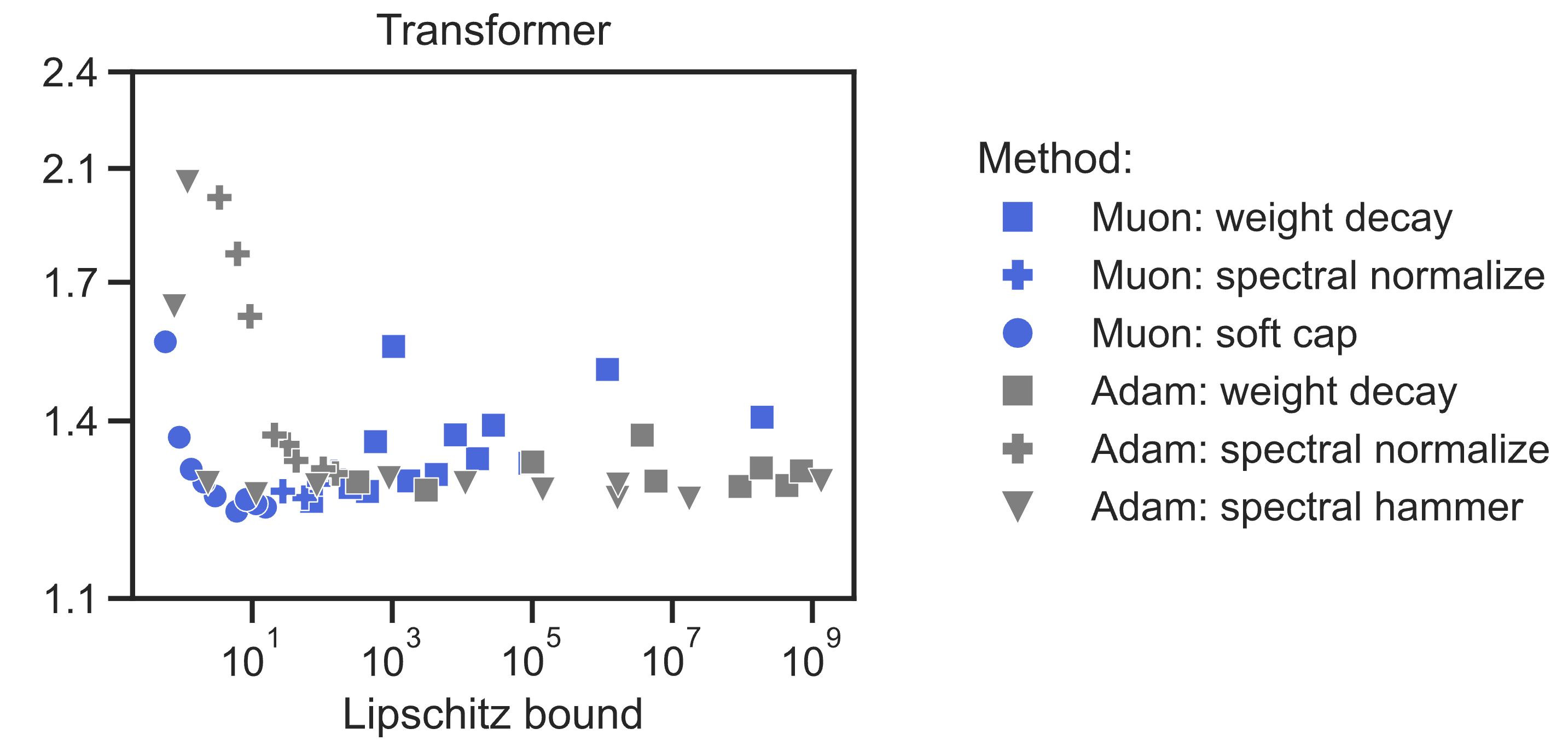
- We were able to create performant Lipschitz-enforced transformers at the 145M parameter scale. For instance our <10-Lipschitz transformer reaches accuracy 21% on FineWeb internet text. But to match baseline 39% accuracy requires an (almost comical) input-to-output Lipschitz bound of $10^{264}$. Can you beat it? We think there's lots of room to improve our methods.
But even now we are excited because of smoothness in the internal units of the model. Each layer has a much better Lipschitz bound. Representations evolve smoothly layer to layer. And _activation norms_ stay smaller when regulating weight norm: the max activation entry is ~100 compared to ~1000 in the baseline (which is already Lipschitz). Bounded activations could improve training stability or low-precision inference.
### Early days
Just over a week ago, Jianlin Su and his team published [MuonClip](https://moonshotai.github.io/Kimi-K2/), which directly constrains the attention $Q$ and $K$ norms at the 1T parameter scale. This idea is brilliant, because it _dynamically_ regulates the weight norm according to a metric—in this case, "max logit" in attention.
I think there's so much potential here. One problem with our method is we constrained all the weights a fixed amount, and that might overburden the model. Our NanoGPT transformers can take 4x as long to reach the same loss. Dynamic contraints—validated at the 1T parameter scale—feel like a very promising direction.
So it really feels like early days. Muon is strong because of the community that has pushed it forward. There is a lot more to do and discover in fast, stable training. And you could be part of the next step.
_Thank you to Jeremy Bernstein, Jordan Juravsky, Kwangjun Ahn, Phillip Isola, Leloy Kun, Adrian Rodriguez-Munoz, Juan Cervino, and Dana Manor for feedback._